Cómo dibujar una escala gráfica

La escala es una proporción y se puede dibujar.

En primer lugar hay que comprender que la notación de escala es una fracción que compara dos tamaños, el tamaño del dibujo respecto del tamaño real de lo dibujado, es decir

E = lo que ocupa en el papel : lo que mide en la realidad

Gráficamente obtendríamos un segmento donde la medida real es el nº que vamos a utilizar para medir.

EJEMPLOS

Utilizando el cm como módulo

E= 1:100

Cogeríamos con el compás 1 cm desde cero y en la medida real podríamos 100.

E= 3:7

Cogeríamos con el compás desde cero 1 cm 3 veces (3x1cm) y en la medida real podríamos 7.

E= 8:3

Cogeríamos con el compás 1 cm 8 veces (8x1cm) y en la medida real podríamos 3.

Lo siguiente es tener claro que la escala gráfica es una regla y por tanto debemos poner suficientes medidas reales para poder medir correctamente con ella (y el compás) así como subdivisiones (contraescala, a la izquierda del cero) para obtener una medición más precisa.

Esto supone tener en cuenta cómo contamos de forma rápida: De uno en uno, de 2 en 2, de 5 en 5, de 10 en 10, de 20 en 20, de 25 en 25, de 50 en 50, de 100 en 100, de 500 en 500, de 100 en 100...

Y supone también tener en cuenta el tamaño del segmento que nos ha quedado, pues si es del tamaño cm o mayor podremos dividirlo en 10 partes iguales pero si resulta más pequeño que el cm tendremos que dividirlo en menos trozos.

Para hacer la contraescala pasamos con el compás el segmento al lado izquierdo del cero. Y lo dividimos en partes iguales (aplicando Teorema de Tales si hacemos operación gráfica). Cada subparte será la precisión conseguida.

En la presentación se pueden ver distintos pasos para dibujar cada ejemplo dado, hasta una opción de aspecto final.

Dibujar escalas gráficas de ranabria

Guada, 2020

¿INSCRIBE O CIRCUNSCRIBE?

 Los dos términos se refieren a cómo se relacionan espacialmente una circunferencia y un polígono, cuando tienen puntos en común.

Si los vértices del polígono están en una circunferencia, el polígono está circunscrito por la circunferencia. En este caso, vemos cómo la circunferencia es la que "abraza" al polígono. Mientras que el polígono es el "abrazado", es decir está inscrito.

Si la circunferencia toca a cada lado del polígono, esto solo es posible cuando la circunferencia es la "abrazada", por tanto ella está circunscrita por el polígono. Mientras, el polígono que es quien abraza tiene a la circunferencia inscrita y por tanto tangente interior.

Resumiendo: "circunscribe lo que abraza, se inscribe lo abrazado".

El punto de vista nos dirá qué buscamos y por tanto qué término debemos utilizar.

1. Dada una circunferencia.... inscribe un polígono en ella. O bien circunscribe un polígono.
2. Dado un polígono.... inscribe una circunferencia. O bien dado un polígono circunscribe una circunferencia.

El punto de vista del polígono es el que nos puede guiar mejor, y teniendo en cuenta los puntos notables de un triángulo llamados circuncentro e incentro.

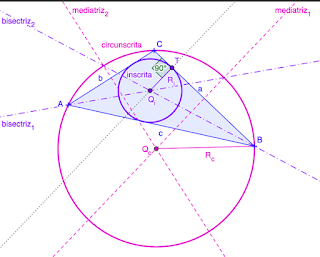
Si queremos trazar circunferencia circunscrita, la que pasa por los vértices, buscaremos el circuncentro. Si las mediatrices de todos los lados se cortan en un mismo punto, ese es el centro de la circunferencia circunscrita. Entonces, el polígono es circunscrito por una circunferencia, pero también está inscrito en  la circunferencia.

Si queremos trazar circunferencia inscrita, la que es tangente interior a los lados del polígono, hallaremos el incentro. Si todas las bisectrices se cortan en un mismo punto, ese es el centro de la circunferencia inscrita. Una vez trazada, el polígono es el circunscrito y la circunferencia la inscrita.

POLÍGONOS Y CIRCUNFERENCIAS INSCRITA Y CIRCUNSCRITA

Hay cierto tipo de polígonos a los que se les puede inscribir y circunscribir circunferencia, mientras que a otros solo una de ellas o bien ninguna de ambas. 

• TRIÁNGULOS. Tienen incentro y circuncentro. Por tanto se pueden inscribir y circunscribir.
• POLÍGONOS REGULARES. También tienen incentro y circuncentro. Se pueden inscribir y circunscribir. Esta característica permite que para construir polígonos regulares se utilice de forma habitual el dato de la circunferencia circunscrita, tanto para método particular como para método general.
• POLÍGONOS REGULARES ESTRELLADOS. Se pueden inscribir en circunferencia pero no tendrán circunferencia inscrita debido a los ángulos cóncavos.
• POLÍGONOS IRREGULARES. Si tienen incentro, se podrán inscribir y si tienen circuncentro se podrán circunscribir. Ambas cualidades a la vez no se darán en los que tengan más de 3 lados y la mayoría de los polígonos irregulares carece de incentro y circuncentro.

Guada, 2020

PROPIEDAD DE TRIÁNGULOS: SUMA DE LADOS

Esta propiedad se explica al sumar lados de un triángulo cualquiera para construir otro triángulo que es isósceles y adyacente del inicial. 

La relación geométrica creada entre ambos triángulos es la siguiente:

• La mediatriz del lado desigual pasa por el vértice que parte la suma de lados.
• El ángulo que se repite en el isósceles, es la mitad del ángulo del triángulo inicial, en el vértice que parte la suma.

 

Guada, 2020