martes, 29 de diciembre de 2020
Cómo dibujar una escala gráfica
viernes, 25 de diciembre de 2020
¿INSCRIBE O CIRCUNSCRIBE?
Los dos términos se refieren a cómo se relacionan espacialmente una circunferencia y un polígono, cuando tienen puntos en común.
Si los vértices del polígono están en una circunferencia, el polígono está circunscrito por la circunferencia. En este caso, vemos cómo la circunferencia es la que "abraza" al polígono. Mientras que el polígono es el "abrazado", es decir está inscrito.
Si la circunferencia toca a cada lado del polígono, esto solo es posible cuando la circunferencia es la "abrazada", por tanto ella está circunscrita por el polígono. Mientras, el polígono que es quien abraza tiene a la circunferencia inscrita y por tanto tangente interior.
Resumiendo: "circunscribe lo que abraza, se inscribe lo abrazado".
El punto de vista nos dirá qué buscamos y por tanto qué término debemos utilizar.
- Dada una circunferencia.... inscribe un polígono en ella. O bien circunscribe un polígono.
- Dado un polígono.... inscribe una circunferencia. O bien dado un polígono circunscribe una circunferencia.
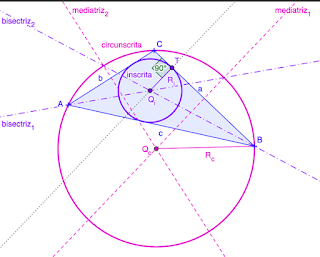
Si queremos trazar circunferencia circunscrita, la que pasa por los vértices, buscaremos el circuncentro. Si las mediatrices de todos los lados se cortan en un mismo punto, ese es el centro de la circunferencia circunscrita. Entonces, el polígono es circunscrito por una circunferencia, pero también está inscrito en la circunferencia.
Si queremos trazar circunferencia inscrita, la que es tangente interior a los lados del polígono, hallaremos el incentro. Si todas las bisectrices se cortan en un mismo punto, ese es el centro de la circunferencia inscrita. Una vez trazada, el polígono es el circunscrito y la circunferencia la inscrita.
POLÍGONOS Y CIRCUNFERENCIAS INSCRITA Y CIRCUNSCRITA
Hay cierto tipo de polígonos a los que se les puede inscribir y circunscribir circunferencia, mientras que a otros solo una de ellas o bien ninguna de ambas.
- TRIÁNGULOS. Tienen incentro y circuncentro. Por tanto se pueden inscribir y circunscribir.
- POLÍGONOS REGULARES. También tienen incentro y circuncentro. Se pueden inscribir y circunscribir. Esta característica permite que para construir polígonos regulares se utilice de forma habitual el dato de la circunferencia circunscrita, tanto para método particular como para método general.
- POLÍGONOS REGULARES ESTRELLADOS. Se pueden inscribir en circunferencia pero no tendrán circunferencia inscrita debido a los ángulos cóncavos.
- POLÍGONOS IRREGULARES. Si tienen incentro, se podrán inscribir y si tienen circuncentro se podrán circunscribir. Ambas cualidades a la vez no se darán en los que tengan más de 3 lados y la mayoría de los polígonos irregulares carece de incentro y circuncentro.
lunes, 7 de diciembre de 2020
PROPIEDAD DE TRIÁNGULOS: SUMA DE LADOS
- La mediatriz del lado desigual pasa por el vértice que parte la suma de lados.
- El ángulo que se repite en el isósceles, es la mitad del ángulo del triángulo inicial, en el vértice que parte la suma.
Guada, 2020
sábado, 7 de noviembre de 2020
TRASLADAR UN ÁNGULO CON EL COMPÁS
Para trasladar un ángulo con el compás se hace un primer arco con centro en el vértice dado y se repite con el mismo radio en el nuevo vértice. Después se toma con el compás la distancia entre los puntos de intersección del arco con los lados del ángulo dado y se pasa a la nueva posición. Los pasos son similares a la construcción de un triángulo isósceles, donde el lado desigual es la distancia entre dichas intersecciones.
viernes, 6 de noviembre de 2020
RECTÁNGULO
Es un cuadrilátero paralelogramo que tiene todos los ángulos iguales de amplitud 90º y los lados opuestos iguales 2 a 2. Sus diagonales son iguales y se cortan en el punto medio, punto por el que también pasan las mediatrices de los lados. Esto permite que el polígono sea inscriptible en una circunferencia y por tanto que se pueda dibujar la circunferencia circunscrita al rectángulo.
ROMBO
El rombo es un cuadrilátero paralelogramo que tiene los 4 lados iguales y los ángulos iguales 2 a 2. Sus diagonales son desiguales y perpendiculares, siendo cada una mediatriz de la otra. Además, son bisectriz de los ángulos que dividen lo cual permite el trazado de la circunferencia inscrita, con centro en la intersección de las diagonales.
sábado, 9 de mayo de 2020
Triángulo equilátero en plano oblicuo dada altura
Triangulo equilátero en plano oblicuo y con lados en planos de proyección
Esto supone que cada uno de esos dos lados deberá pertenecer a la traza del plano oblicuo correspondiente.
- Lado en el plano vertical de proyección, en la traza vertical del plano oblicuo.
- Lado en el plano horizontal de proyección, en la traza horizontal del plano oblicuo.
Como ambas trazas deberán cortarse en la Linea de Tierra, uno de los vértices del triángulo estará ahí. El segundo vértice se sitúa a la distancia lado en la traza vertical dada.
Para visualizarlo se puede hacer un montaje en 3D con un cartabón que haría del plano oblicuo dado, con el triángulo en la posición descrita.
sábado, 18 de abril de 2020
Cómo dibujar en perspectiva: tipos de perspectiva habituales
- Qué tipo de perspectiva
- Disposición de los ejes
- Punto de vista elegido
- Escala a la que se pide el dibujo
- Reducción en los ejes
- Pruebas a mano alzada
- Qué tipo de perspectiva
- Perspectivas cilíndricas (rayos proyectantes paralelos). Las más utilizadas son la isométrica de proyección perpendicular y la caballera de proyección oblicua. Son perspectivas de rápida ejecución pero el realismo es menor que en las cónicas.
- Perspectivas cónicas (rayos proyectantes divergentes). Son habituales la central (de 1 punto de fuga) y la oblicua de 2 puntos de fuga. Son perspectivas más elaboradas y que la visión de un ojo humano.
En cualquiera de estas perspectivas, el eje z vertical se dibujará siempre en posición vertical (en la perspectiva militar, sin embargo, el eje z varía su inclinación).
- Disposición de los ejes.
- Oblicuidad, luego reducción. Miremos lo que ocupa un brazo por ejemplo, en un espejo. Vemos con el brazo estirado y en paralelo al espejo su longitud máxima (largo del brazo), pero a medida que el brazo, bien estirado, lo enfocamos hacia el espejo, parece acortarse y si lo ponemos totalmente perpendicular su longitud habrá desaparecido (la mano tapa todo el brazo). Esto se resuelve en perspectiva aplicando una reducción, en el eje que esté dispuesto de posición oblicua respecto del plano del cuadro.
- Cerca-lejos, luego reducción paulatina. Se trata de un gradiente de reducción que sirve tanto para la oblicuidad como para la situación de objetos a diferentes distancias y que determinarán que aunque sean iguales de tamaño se vean más pequeños cuanto más lejos estén. Es el concepto de profundidad aplicado con mayor realismo. Y este contexto lo ofrece la perspectiva cónica gracias al centro de la radiación situado en el supuesto ojo del espectador -claramente no hay 2 ojos por lo que la visión binocular humana es imitada parcialmente-. La perspectiva cónica es la más utilizada por los artistas, a veces de forma intuitiva y otras con verdadera fidelidad técnica.
En perspectiva isométrica sucede lo mismo
Al dibujar en perspectiva se nos exige un esfuerzo de visión espacial. Y si la construcción es correcta, la lectura será coherente y sencilla.
Caballera. El eje y se puede cambiar de posición pues la dirección de proyección sobre el plano del cuadro puede ser cualquiera. Sea el ángulo que sea el que dibuje el eje y con el x y con el z, tendremos que interpretarlo de 90º. En cuanto al ángulo xz, se ve en verdadera magnitud, dado el paralelismo entre el plano del cuadro y el espectador.
Isométrica. La dirección de los 3 ejes es fija. La disposición equidistante de la angulosidad de cada eje en el espacio respecto del plano del cuadro determina una intersección de puntos equidistantes que son los vértices de un triángulo equilátero, el triángulo de las trazas. Los ejes proyectados forman las alturas de ese triángulo y dibujan ángulos de 120º.
- Punto de vista elegido
En la cónica central, al igual que en caballera, el espectador se sitúa paralelo a una cara de la pieza.
- Escala a la que se pide el dibujo
- Reducción en los ejes. Coeficiente de reducción.
- Pruebas a mano alzada
TRAS DECIDIR QUÉ PERSPECTIVA, QUÉ DISPOSICIÓN DE EJES, QUÉ POSICIÓN PARA LA PIEZA (dirección del alzado), trabaja la visualización de la pieza, a mano alzada. Hasta que entiendas bien su forma 3D. Te será útil tener en cuenta las dimensiones máximas, es decir el prisma en que estaría encajado su volumen. Lo siguiente será trabajar con líneas paralelas a los ejes, analizar la pieza por otros prismas que la configuren (puzzle tridimensional), tener en cuenta ejes de simetría y otras relaciones geométricas.
miércoles, 8 de abril de 2020
Simetría
- Simetría bilateral o de eje.
- Simetría radial o central.
En la simetría radial o central, estaríamos en una homotecia donde el valor también sería k= -1. De nuevo el valor negativo indica al otro lado, en este caso del centro de homotecia. Y la proporción de la unidad también se refiere a la escala natural (equidistancia). Aquí las direcciones de los pares de puntos simétricos son divergentes desde el centro de homotecia que es el centro de la radiación.
Trazado de simetría artística
Una técnica sencilla para dibujar figuras simétricas es utilizando dobleces en papel. Con un solo doblez se consigue 1 eje de simetría.
En el caso de simetría central. Necesitaríamos varios dobleces de papel, dejando el centro de simetría en el centro de la hoja.
Otra técnica es calcar la figura después de darle vuelta al papel (este es el mismo efecto que el selfie).
Y lo más sencillo de todo: utilizar un programa de ordenador que permita hacer simetría.